МОДЕЛЮВАННЯ ДИНАМІКИ СЕРЕДНЬОЇ ЗАРОБІТНОЇ ПЛАТНІ В УКРАЇНІ ЗА ДОПОМОГОЮ THRESHOLD РЕГРЕСІЇ
УДК 331.28
Морозова К.А., студентка 2 року ОС магістр
ХНЕУ ім. С. Кузнеця
Анотація. У статті розглянуто питання моделювання процесів формування трудових доходів населення України. Було побудовано комплекс моделей, що дозволяють дослідити вплив мінімальної заробітної плати на середню. За допомогою моделей threshold регресії знайдено перехідні точки у динаміці мінімальної заробітної плати, що мали вплив на тенденцію зросту середньої.
Ключові слова: трудові доходи населення, середня заробітна плата, мінімальна заробітна плата, лінійна регресія, threshold регресія, threshold ефекти, R.
Abstract. The article deals with the modeling of the formation processes of labor incomes of the Ukraine’s population. The comlex of models was developed to investigate the impact of the minimum wage on average. The transition points were found by regression threshold models in the dynamics of the minimum wage, which had an effect on the tendency of average growth.
Keywords: labor incomes of the population, average salary, minimal salary, linear regression, threshold regression, threshold effects, R.
Рівень доходів населення є найважливішим показником його добробуту. Основними чинниками, що впливають на величину доходів, є: динаміка роздрібних цін, рівень податків, насиченість ринку споживчими товарами та інші. Але центральне місце в трудових доходах населення займає заробітна плата. Відповідно до закону України «Про оплату праці», заробітна плата – це винагорода, обчислена, як правило, у грошовому виразі, яку за трудовим договором роботодавець виплачує працівникові за виконану ним роботу [1]. Заробітна платня є найбільш чуттєвим індикатором змін загальної економічної ситуації в цілому.
Одним з прямих методів регулювання державою процесів формування трудових доходів населення, зокрема заробітної плати, є інститут мінімальної заробітної плати. Істотні зміни в розмірі цього показника можуть мати неабиякий вплив на розмір середньої заробітної плати, за якою зазвичай оцінюється стан добробуту населення країни загалом.
В Україні над питаннями оцінки динаміки формування показників середньої заробітної плати працювали такі вчені, як В. Геєць, Е. Лібанова, Н. Болотіна, І. Новак, О. Івахненко, Н. Кизим, Н. Павловська, В. Приймак та ін. Однак все ще мало вивченим залишається аспект впливу на середню заробітну плату різких змін мінімальної заробітної плати.
Таким чином, метою дослідження є моделювання динаміки середньої заробітної платні в Україні з урахуванням впливу на неї численних змін розміру мінімальної заробітної плати в країні.
Гіпотеза дослідження полягає в наступному: різки чи занадто великі зміни мінімальної заробітної платні можуть призводити до зміни загального тренду у формуванні показника середньої заробітної плати в Україні.
Основним інструментом, що буде застосовано для перевірки гіпотези, виступають моделі threshold регресії, призначені для виявлення точок переходу, які виступають перемикачем між режимами у динаміці часового ряду. Порогові (threshold) регресійні моделі – це клас моделей регресії, де незалежні зміні пов’язані з результатами залежно від порога. Вводячи пороговий параметр, також відомий як точка зміни, моделі порогової регресії забезпечують простий спосіб моделювання певних видів нелінійних відносини між результатом та предиктором [2]. Threshold регресія більш конкурентна порівняно з іншими методами нелінійної регресії, тому що не вимагає початкового значення для точки зміни і знаходить глобальне оптимальне рішення з найбільшою вірогідністю. Конкретним прикладом моделі є модель threshold регресії, розроблена Хансеном [2]. Порогова оцінка Хансена базується на двох структурних рівняннях режиму наступним чином (1, 2):
\[ y_{t} = \theta_{1}x_{t} + e_{1t}\ iakshcho\ q_{t} \leq \gamma\ ,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( 1 \right) \]
\[ y_{t} = \theta_{1}x_{t} + e_{1t}\ iakshcho\ q_{t} > \gamma\ ,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( 2 \right) \]
де \(\gamma\) позначає порогове значення,
\(y\) – залежна змінна,
\(x\) – незалежна змінна,
\(q\) – порогова змінна,
\(\text{ θ}\) – коефіцієнт нахилу,
\(e\) – термін помилки.
Порогове значення невідоме апріорі. Тому його слід оцінювати разом з іншими параметрами. Коли порогова змінна є меншою, ніж порогове значення, модель продовжує оцінювати рівняння (1). З іншого боку, коли порогова величина перевищує порогове значення, модель оцінює рівняння (2) [3].
Моделі порогової регресії можуть мати різні форми в залежності від того, що відбувається на порозі [4]. На рис. 1 показані чотири типи порогових ефектів: крок (step), шарнір (hinge), сегментований (segmented), «stegmented».
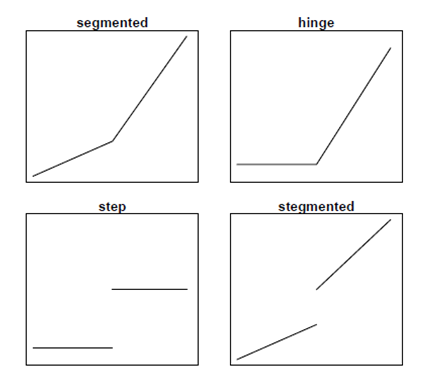
Рис. 1. Типи ефектів моделі порогової регресії
У рамках узагальненої лінійної регресії можна записати середню функцію цих чотирьох типів порогових моделей наступним чином (3, 4, 5, 6):
\[ \eta = \alpha_{1} + \alpha_{2}^{T}z + \beta_{1}I\left( x > e \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ - step,\ \ \ \ \ \ \ \ \ \ \ \ \ \left( 3 \right) \]
\[ \eta = \alpha_{1} + \alpha_{2}^{T}z + \beta_{1}\left( x - e \right)_{+}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ - hinge,\ \ \ \ \ \ \ \ \ \ \ \ \ \left( 4 \right) \]
\[ \eta = \alpha_{1} + \alpha_{2}^{T}z + \beta_{1}\left( x - e \right)_{+} + \gamma x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ - segmented,\ \ \ \ \ \ \ \ \ \ \ \ \ \left( 5 \right) \]
\[ \eta = \alpha_{1} + \alpha_{2}^{T}z + \beta_{1}\left( x - e \right)_{+}{+ \gamma x + \beta}_{2}I\left( x > e \right)\ \ - stegmented,\ \ \ \ \ \ \ \ \ \ \ \ \ \left( 6 \right) \]
де \(e\) – порогове значення; \(x\) – параметр регресії, який досліджується на наявність порогу; \(z\) – інші параметри регресії; \(I\left( x > e \right) = 1\) при \(x \geq e\), та 0, якщо \(x \leq e\); \(\left( x - e \right)_{+} = x - e\) при \(x \geq e\), та 0, якщо \(x < e\).
Для вибору специфікації моделі для опису динаміки формування показника середньої заробітної плати було побудовано ряд моделей лінійної регресії. Серед моделей було обрано дві за критерієм найвищого значення коефіцієнту детермінації, мінімізації помилок та статистичної значущості параметрів, а саме:
\[\text{meanZP} = a_{0} + a_{1}*t + a_{2}*t^{2} + a_{3}*\text{minZP},\]
\[\text{meanZP} = a_{0} + a_{1}*t + a_{2}*t^{2} + a_{3}*\log\text{minZP},\]
де \(\text{meanZP}\) – значення середньої заробітної плати;
\(\text{minZP}\) – значення мінімальної заробітної плати;
\(\log\text{minZP}\) – значення логарифму мінімальної заробітної плати;
\(t\) – показник часу.
Обрані специфікації моделей було протестовано на наявність перехідних точок за допомогою побудови моделей порогової регресії і різними ефектами на їх основі.
Серед моделей порогової регресії за основним показником якості прогнозу середньої абсолютної процентної похибки (MAPE) із значенням 6,64% найкращою вважається модель із ефектом step. Ця модифікація моделі єдина вказала на значення мінімальної заробітної плати 1450 грн, що належить до періоду кінця 2016 року. Перехідний етап у цьому випадку наступає коли заробітна плата спочатку зросла до 1650 грн, через місяць збільшилась у 2 рази із січня 2017 року. Ніколи зріст мінімальної заробітної не був таким сильним за умови стабільних темпів інфляції, як в січні 2017 року, коли вона була піднята на 100%. Це дійсно можна вважати стрибком у тенденції росту мінімальної заробітної плати, однак цей стрибок не вплинув на зміну тенденції зросту середньої заробітної плати. Наступне підвищення мінімального розміру оплати праці з 3200 до 3723 грн відбулося з 1 січня поточного року і склало 16%. Це зростання стало другим за величиною з 2010 року.
Також дуже гарний результат оцінки помилок прогнозу має модель порогової регресії з ефектом hinge (MAPE = 6,72%). У ході аналізу результатів цієї моделі виявилось, що точка переходу впливу мінімальної заробітної плати на середню спостерігається наприкінці 2013 року. Моделі з іншими пороговими ефектами segmented та stegmented дали точно такі ж значення точок переходу. Це 1218 грн, що дорівнює 7,105 у логарифмічному виразі. Це значення пов’язане із періодом політично-соціальної нестабільності в Україні. Мінімальна заробітна плата у той час збільшилась у 1,06 разів, середня у 1,11 порівняно з попереднім місяцем. Аналізуючи динаміку збільшення середньої заробітної плати у річному інтервалі з моменту цього перехідного значення, можна відмітити, що дійсно цей стрибок є максимальним, а значення до й після менші, наприклад, зменшення темпів росту до 0,87 вже у січні 2014 року. Отже, на відміну від моделі step, тут спостерігається зміна тенденції динаміки середньої заробітної плати, що підтверджує ідею цього виду threshold моделі, представлену на рис. 1.
Таким чином використання моделей порогової регресії дозволило підтвердити гіпотезу про наявність порогового значення для мінімальної заробітної плати при моделюванні динаміки показника середньої заробітної плати в України. Крім того, важливим аспектом результатів моделювання є те, що ці моделі порогової регресії є достатньо якісними та придатні для побудови прогнозів високої точності.
ЛІТЕРАТУРА
Permar S.R. hiv-1 envelope–specific antibody responses and reduced risk of perinatal transmission / Fong Y., Vandergrift N., Fouda G.G., Gilbert P., Parks R., Jaeger F.H., Pollara J., Martelli A., Liebl B.E., Lloyd K., Yates N.L., Overman R.G., Shen X., Whitaker K., Chen H., Pritchett J. Maternal. J. Clin Investig. – 2015. – 125(7): – Pp. 2702–06.
Wakefield J. Bayesian and Frequentist Regression Methods. Springer Series in Statistics Series. New York: Springer, 2012. – Pp. 45-67.
Pastor-Barriuso R. / Guallar E, Coresh J. Transition models for change-point estimation in logistic regression. Stat Med. – 2003. – 22(7): – Pp. 1141–62.
Науковий керівник
к.е.н., доцент Івахненко О.В.